暴力递归到动态规划(一):Robot to Target And Two Wise Pocker Men

dp表的本质:调用M个子函数&&每一次传参有K个可变量👇
建立并维护M个K维表格

本文所有gpt回答都由gpt4生成

Robot Goes to Target

题目一:

---

完全暴力递归

int baoli(int cur, int rest, int target, int length) {
	if (length == 1) rest == 0? 1: 0;
	if (rest == 0) return (cur == target) ? 1 : 0;
	if (cur == 1) return baoli(2, rest - 1, target, length);
	if (cur == length) return baoli(length - 1, rest - 1, target, length);
	return baoli(cur + 1, rest - 1, target, length) + baoli(cur - 1, rest - 1, target, length);;
}

傻缓存法

{main}vector<vector<int>> dp(N + 1, vector<int>(R + 1, -1));

int process(int cur, int rest, int target, int length, vector<vector<int>> dp) {
	if (length == 1) return rest == 0? 1: 0;
	if (dp[cur][rest] != -1)  return dp[cur][rest];
	//之前没算过!

	int ans = 0;
	if (abs(target - cur) > rest) ans = 0;
	else if (rest == 0) ans = (cur == target) ? 1 : 0;
	else if (cur == 1) ans = process(2, rest - 1, target, length, dp);
	else if (cur == length) ans = process(length -1, rest - 1, target, length, dp);
	else ans = process(cur + 1, rest - 1, target, length, dp) + process(cur - 1, rest - 1, target, length, dp);
	dp[cur][rest] = ans;
	return ans;
}

逆向直接dp表外挂法

int zhengbiaoshengcheng(int cur, int rest, int target, int length) {
	if (length == 1) return rest == 0 ? 1 : 0;
	vector<vector<int>> dp1(length + 1, vector<int>(rest + 1, 0));
	dp1[target][0] = 1;

	for (int i = 1; i <= rest; i++) {
		dp1[1][i] = dp1[2][i - 1];
		for (int j = 2; j < length; j++)
			dp1[j][i] = dp1[j + 1][i - 1] + dp1[j - 1][i - 1];
		dp1[length][i] = dp1[length - 1][i - 1];
	}
	return dp1[cur][rest];
}

原理一句话: 由 "纯暴力"(第一个解法) 法进一步修正得到 . 直接上图

dp递推法原理

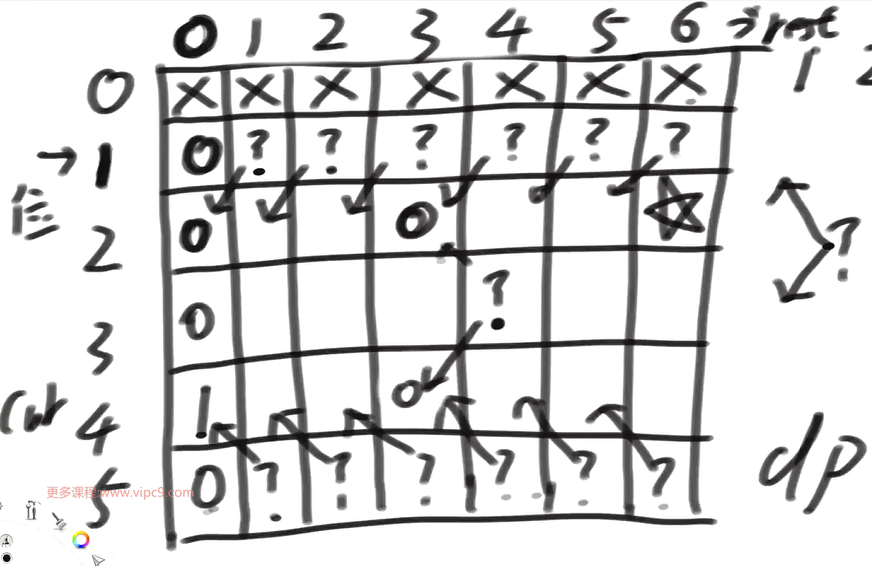
先把第一列填好, 然后从左往右, 从上到下, 根据暴力方法的代码 所推导出格子之间的依赖, 把数值填好. 最后, 返回dp1[cur][rest];

入参判断&&分析bug来源

为什么进入函数第一要判断length?

　　注意: 如果所有其他的数据都合理, 当N == 1, 且 R != 0, 答案应该为 0 .
　　如果不这么设置, 会出现”vector subscript out of range”, 即 数组下标 超出范围. 因为, 在”dp外挂” 这一种解法中, 会用到dp1[1][i] = dp1[2][i-1]. 如果 1 ==length , 那么 显然会产生越界.
　　我是怎么发现的呢? 用对数器反复实验, 总有那么几次(大概100次有一次)会导致 报上面提到的错, 于是, 我以30为单位, 重复执行程序, 打印出每一次得到的四个随机整数, 停下来的那一次就是出错的数组. 于是, 我得到了三组数(从左到右依次为:初始位置,剩余步数,目标位置,活动范围):
1 8 1 1
1 1 1 1
1 2 1 1
　　不难发现, 第一个和最后一个数都是1的时候, 程序出错(当然这种观察方式过于原始且有赌博性质). 进一步分析, 由于初始位置一定小于活动范围, 即初始位置由活动范围所控制/界定, 所以, 问题就出在了活动范围!
　　怎么办? 向我之前那样, 全部都检查一下, 就好啦!
　　其实还有一种发现的方法：由于我一开始N的取值范围是1~100,所以N取到1的期望就是1/100.😄

用对数器看着Test Over. 跑完, 真爽!🤭

over

---

下面, 是带对数器的完整的代码~

#include <bits/stdc++.h>

using namespace std;

void set4nums(int& M, int& R, int& T, int& N) {
    N = rand() % 30 + 1;
    M = rand() % N + 1;
    if (M > N) {
        M ^= N;
        N ^= M;
        M ^= N;
    }
    T = rand() % N + 1;
    R = rand() % 10;
}

int baoli(int cur, int rest, int target, int length) {
    if (length == 1)
        return rest == 0 ? 1 : 0;
    if (rest == 0)
        return (cur == target) ? 1 : 0;
    if (cur == 1)
        return baoli(2, rest - 1, target, length);
    if (cur == length)
        return baoli(length - 1, rest - 1, target, length);
    return baoli(cur + 1, rest - 1, target, length) + baoli(cur - 1, rest - 1, target, length);
    ;
}

int process(int cur, int rest, int target, int length, vector<vector<int>> dp) {
    if (length == 1)
        return rest == 0 ? 1 : 0;
    if (dp[cur][rest] != -1)
        return dp[cur][rest];
    // 之前没算过!

    int ans = 0;
    if (abs(target - cur) > rest)
        ans = 0;
    else if (rest == 0)
        ans = (cur == target) ? 1 : 0;
    else if (cur == 1)
        ans = process(2, rest - 1, target, length, dp);
    else if (cur == length)
        ans = process(length - 1, rest - 1, target, length, dp);
    else
        ans = process(cur + 1, rest - 1, target, length, dp) + process(cur - 1, rest - 1, target, length, dp);
    dp[cur][rest] = ans;
    return ans;
}
//  1 8 1 1
//  1 1 1 1
//  1 2 1 1
int zhengbiaoshengcheng(int cur, int rest, int target, int length) {
    if (length == 1)
        return rest == 0 ? 1 : 0;
    vector<vector<int>> dp1(length + 1, vector<int>(rest + 1, 0));
    dp1[target][0] = 1;

    for (int i = 1; i <= rest; i++) {
        dp1[1][i] = dp1[2][i - 1];
        for (int j = 2; j < length; j++)
            dp1[j][i] = dp1[j + 1][i - 1] + dp1[j - 1][i - 1];
        dp1[length][i] = dp1[length - 1][i - 1];
    }
    return dp1[cur][rest];
}

int main() {
    srand(time(0));
    int test = 10000;
    while (test--) {
        int M, R, T, N;
        set4nums(M, R, T, N);
        int bao = baoli(M, R, T, N);
        vector<vector<int>> dp(N + 1, vector<int>(R + 1, -1));
        int pro = process(M, R, T, N, dp);
        int zheng = zhengbiaoshengcheng(M, R, T, N);
        if (pro != zheng || pro != bao) {
            cout << "Oops!" << endl;
            cout << M << R << T << N;
        }
        return 0;
    }
}

以下是对于学习编程以来的遗留问题的解决

行列如何分清? 如何更好地定义行列?

ME
我感到非常疑虑, 因为我真的感觉行和列的区别很难分清, 也很难界定. 因为, 好像任何二维数组的横纵坐标可以互换, 只要代码做出相应调整, 还是能实现同样的功能. 我想知道, 如果有两个变量, 我应该如何确定它们代表行(第一个参数)还是列(第二个参数)呢?

GPT

理解行和列，特别是在编程的上下文中，确实可能会引起困惑。但记住，行和列更多是一个习惯和传统的约定，而不是一个固定的规则。以下是一些建议，帮助你区分和使用它们：

思考数据的实际意义：

有时，数据的本质会为你提供线索。例如，假设你有一个二维数组，表示学生的分数，其中每行代表一个学生，每列代表一个科目。在这种情况下，学生的数量自然地变成了行数，而科目的数量变成了列数。

考虑存储的效率和方便性：

在某些算法或数据处理任务中，访问数组的方式可能会使得选择一个布局比另一个布局更加有效。例如，如果你经常需要处理每个学生的所有成绩，那么按行存储（每行一个学生）可能更有意义。相反，如果你经常需要处理所有学生的某一科的成绩，那么按列存储可能更合适。

约定俗成的使用：

在许多编程语言和文档中，二维数组或列表通常都是先行后列的。这也是为什么我们在讨论屏幕坐标或像素时，经常说“y坐标（或行）和x坐标（或列）”。

注释和命名：

如果你对行和列的用途感到不确定或容易混淆，给变量使用清晰的名称和注释是很有帮助的。例如，numStudents 和 numSubjects 比简单的 rows 和 cols 提供了更多的上下文信息。

思考可读性：

在许多情况下，将数据组织成行和列是为了代码的可读性和组织性。如果交换行和列会使代码更容易理解，那么就这样做。

最后，你是对的，行和列通常是可以互换的，特别是在编程的上下文中。但如何选择行和列通常取决于具体的应用和你希望如何组织和处理数据。

ME
像这个例子, 我真的没有一套熟练的思路和逻辑 , 应该是让横纵坐标代表rest 还是代表机器人的移动范围N,
两种分配方式各有什么优劣?

GPT

对于动态规划问题，如何选择行和列来代表你的状态是一个常见的问题。正确地组织你的dp数组可以使问题更加直观和易于理解，但可能的组织方式不止一种，并且每种方式都有其优势和劣势。

首先，让我们分析你给出的机器人走路问题的代码：

在这里，dp1[j][i]被定义为：

j 代表当前的位置。
i 代表剩余的步数。
dp1[j][i] 代表从位置 j 开始，还有 i 步要走，到达 target 的方法数。

现在，我们来讨论两种可能的组织方式：

rest 作为行，位置作为列（如你的代码所示）:
优势:
很容易以步数为单位迭代，特别是当步数是主要的迭代维度时。
劣势:
某些读者可能觉得机器人的位置更直观作为第一个参数。

位置作为行，rest 作为列:
优势:
对于那些习惯于位置作为主要状态的读者来说，可能更直观。
在某些问题中，这种组织方式可能更容易实现边界条件。
劣势:
你可能需要修改迭代的方式，尤其是如果步数是你的主要迭代维度。

专业建议:
直观性：考虑哪个维度是更自然的迭代选择。例如，如果你发现你经常基于剩余步数进行迭代和计算，那么可能更适合将其放在主维度（即行）。
边界条件：某些组织方式可能会使边界条件更容易处理。考虑不同的组织方式如何影响你的初始化和终止条件。
复杂性和代码可读性：有时，选择一个特定的组织方式会简化代码，使其更易于理解。
注释：无论你选择哪种方式，提供清晰的注释，描述每个维度的含义是很有帮助的。

所以, 到这一步,我就解决了内心的一个长期疑惑, 二维数组的横纵坐标应该如何定义的问题. 于是, 我趁还有热度, 开始把zhengbiaoshengcheng(也就是最后一种dp外挂解法)重新用横纵坐标交换的方式写了一遍, 一气呵成:

int zhengbiaoshengcheng1(int cur, int rest, int target, int length) {
    if (length == 1)
        return rest == 0 ? 1 : 0;
    vector<vector<int>> dp2(rest + 1, vector<int>(length + 1, 0));
    // dp[rest][cur]
    dp2[0][target] = 1;
    for (int i = 1; i <= rest; i++) {
        dp2[i][1] = dp2[i - 1][2];
        for (int j = 2; j < length; j++)
            dp2[i][j] = dp2[i - 1][j + 1] + dp2[i - 1][j - 1];
        dp2[i][length] = dp2[i - 1][length - 1];
    }
    return dp2[rest][target];
}

结束!

二维数组的传递

二维数组的传递

数组指针_确定列数

#include <iostream>

void display(int arr[][5], int rows) {
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < 5; ++j) {
            std::cout << arr[i][j] << " ";
        }
        std::cout << std::endl;
    }
}

int main() {
    int myArray[3][5] = {{1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}, {11, 12, 13, 14, 15}};
    display(myArray, 3);
}

数组指针_列数不确定

void display(int** arr, int rows, int cols) {
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            std::cout << arr[i][j] << " ";
        }
        std::cout << std::endl;
    }
}

int main() {
    int rows = 3, cols = 5;
    int** myArray = new int*[rows];
    for (int i = 0; i < rows; ++i) {
        myArray[i] = new int[cols];
    }

    // Fill and use myArray

    display(myArray, rows, cols);

    // Don't forget to delete memory
    for (int i = 0; i < rows; ++i) {
        delete[] myArray[i];
    }
    delete[] myArray;
}

使用模板

#include <iostream>

template <size_t rows, size_t cols>
void display(int (&arr)[rows][cols]) {
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            std::cout << arr[i][j] << " ";
        }
        std::cout << std::endl;
    }
}

int main() {
    int myArray[3][5] = {{1, 2, 3, 4, 5}, {6, 7, 8, 9, 10}, {11, 12, 13, 14, 15}};
    display(myArray);
}

vector容器

#include <iostream>
#include <vector>

void display(const std::vector<std::vector<int>>& arr) {
    for (const auto& row : arr) {
        for (int num : row) {
            std::cout << num << " ";
        }
        std::cout << std::endl;
    }
}

void addElement(std::vector<std::vector<int>>& arr, int row, int value) {
    if (row < arr.size()) {
        arr[row].push_back(value);
    } else {
        std::vector<int> newRow = {value};
        arr.push_back(newRow);
    }
}

void removeElement(std::vector<std::vector<int>>& arr, int row, int col) {
    if (row < arr.size() && col < arr[row].size()) {
        arr[row].erase(arr[row].begin() + col);
    }
}

int main() {
    std::vector<std::vector<int>> myArray = {{1, 2, 3}, {4, 5}, {6, 7, 8, 9, 10}};

    display(myArray);
    
    std::cout << "\nAfter adding an element to second row:\n";
    addElement(myArray, 1, 11);
    display(myArray);

    std::cout << "\nAfter removing the third element from the first row:\n";
    removeElement(myArray, 0, 2);
    display(myArray);
}

GPT_三种对比

数组指针:

使用指针到指针（例如 int** arr）的方法可以让你在创建函数时不知道数组的大小。但是，这种方法通常需要你手动管理内存，增加了出错的机会。
使用数组的指针（例如 int arr[][cols]）的方法要求你知道至少一维的大小（通常是列数）。这意味着你不能完全在不知道任何维度的大小的情况下使用这种方法。

std::vector:

使用 std::vector<std::vector> 是最灵活的选择。你可以不知道行数和列数就创建和传递它。不同的行可以有不同的大小，并且你可以动态地添加和删除元素。它还自动管理内存，因此你不必担心泄漏。
模板:

使用模板（例如 int (&arr)[rows][cols]）允许你在编译时获取数组的尺寸，但你仍然需要知道至少一维的大小（通常是列数）。

Two Wise Poker Men

题目:

---

完全暴力递归

f函数: 我是先手.我要考虑,拿左边或者右边以后, 我作为后手能拿到的分数, 然后选择较大的那个(所以取max).
g函数: 我是后手.我要在对方拿完以后,尝试拿到剩下的牌中的最多的分数,但是,对方只会让我被迫选择较小的那个(所以取min).

// ways1 : 递归解法

// ways 1
int f1(int* arr, int L, int R) {
    if (L == R)
        return arr[L];
    int p1 = arr[L] + g1(arr, L + 1, R);
    int p2 = arr[R] + g1(arr, L, R - 1);
    return max(p1, p2);
}

int g1(int* arr, int L, int R) {
    if (L == R)
        return 0;
    int p1 = f1(arr, L + 1, R);
    int p2 = f1(arr, L, R - 1);
    return min(p1, p2);
}

int ways1(int* arr, int length) {
    int xianshou = f1(arr, 0, length - 1);
    int houshou = g1(arr, 0, length - 1);
    return max(xianshou, houshou);
}

傻缓存法

这里,dp表格必须要两个, 为什么? 子函数有 f 和 g , 所以每个子函数自己配备一个dp表.

// ways 2
int ways2(int* arr, int length) {
    vector<vector<int>> fmap(length, vector<int>(length, -1));
    vector<vector<int>> gmap(length, vector<int>(length, -1));

    int xianshou = f2(arr, 0, length - 1, fmap, gmap);
    int houshou = g2(arr, 0, length - 1, fmap, gmap);
    return max(xianshou, houshou);
}
int f2(int* arr, int L, int R, vector<vector<int>>& fmap, vector<vector<int>>& gmap) {
    if (fmap[L][R] != -1)
        return fmap[L][R];

    int ans = 0;
    if (L == R)
        ans = arr[L];
    else {
        int p1 = arr[L] + g2(arr, L + 1, R, fmap, gmap);
        int p2 = arr[R] + g2(arr, L, R - 1, fmap, gmap);
        ans = max(p1, p2);
    }
    fmap[L][R] = ans;
    return ans;
}

int g2(int* arr, int L, int R, vector<vector<int>>& fmap, vector<vector<int>>& gmap) {
    if (gmap[L][R] != -1)
        return gmap[L][R];

    int ans = 0;

    if (L != R) {
        int p1 = f2(arr, L + 1, R, fmap, gmap);
        int p2 = f2(arr, L, R - 1, fmap, gmap);
        ans = min(p1, p2);
    }
    gmap[L][R] = ans;
    return ans;
}

严格表递推法

// ways 3 严格表递推
int ways3(int* arr, int length) {
    vector<vector<int>> fmap(length + 1, vector<int>(length + 1, 0));
    vector<vector<int>> gmap(length + 1, vector<int>(length + 1, 0));
    for (int i = 0; i < length; i++)
        fmap[i][i] = arr[i];
    for (int startColumn = 1; startColumn < length; startColumn++) {
        int left = 0;
        int right = startColumn;
        while (right < length) {//行会先超范围
            fmap[left][right] = max(arr[left] + gmap[left + 1][right], arr[right] + gmap[left][right - 1]);
            gmap[left][right] = min(fmap[left + 1][right], fmap[left][right - 1]);

            left++;
            right++;
        }
    }
    return max(fmap[0][length - 1], gmap[0][length - 1]);
}

同样, 对数器跑完. 上完整代码

#include <bits/stdc++.h>

using namespace std;


//generate ramdom array

int* generateramdomarray(int & length) {
	
	length = rand() % 19 + 1;
	int* arr = new int[length];
	for (int i = 0; i < length; i++)
		arr[i] = rand() % 6 + 1;
	return arr;
}


//ways1 : 递归解法
int f1(int* arr, int L, int R);
int g1(int* arr, int L, int R);
int ways1(int* arr, int);

//ways2 : 傻缓存
int f2(int* arr, int L, int R, vector<vector<int>>&, vector<vector<int>>&);
int g2(int* arr, int L, int R, vector<vector<int>>&, vector<vector<int>>&);
int ways2(int* arr, int);

//ways3 : 严格表递推

int ways3(int* arr, int length);

//ways4 : 纯暴力




/*
0 1 1 4 1 3 3 2 5 4 4 2 0
14
16
16
5 3 1 5 0 3
11
13
13*/
 
int main() {
	//int arr[5] = { 1, 5, 3, 2, 4  };
	int arr1[10] = {3, 1 ,6 ,3 ,7 ,29 ,10 , 9 , 8 ,30};
	
	srand(time(0));
	//srand(0);
	int test = 10000;
	while (test--)
	{
		int length = 0;
		int* arr = generateramdomarray(length);
		//for (int i = 0; i < length; i++)
			//cout << arr[i] << " ";
		//cout << endl;

		int w1 = ways1(arr, length);
		int w2 = ways2(arr, length);
		int w3 = ways3(arr, length);
		if (w1 != w2 || w1 != w3) {
			cout << "Oops!";
			cout << w1 << endl;
			cout << w2 << endl;
			cout << w3 << endl;
		}
		delete[] arr;
	}
	cout << "Test Over!" << endl;
	//cout << "in 2 " << endl;
	
	return 0;
}

//ways 1
int f1(int* arr, int L, int R) {
	if (L == R) return arr[L];
	int p1 = arr[L] + g1(arr, L + 1, R);
	int p2 = arr[R] + g1(arr, L, R - 1);
	return max(p1, p2);
}

int g1(int* arr, int L, int R) {
	if (L == R) return 0;
	int p1 = f1(arr, L + 1, R);
	int p2 = f1(arr, L, R - 1);
	return min(p1, p2);
}

int ways1(int* arr, int length) {
	int xianshou = f1(arr, 0, length - 1);
	int houshou = g1(arr, 0, length - 1);
	return max(xianshou, houshou);
}



//ways 2
int ways2(int* arr, int length) {
	vector<vector<int>> fmap(length , vector<int>(length , -1));
	vector<vector<int>> gmap(length , vector<int>(length , -1));

	int xianshou = f2(arr, 0, length-1, fmap, gmap);
	int houshou = g2(arr, 0, length-1, fmap, gmap);
	return max(xianshou, houshou);
}
int f2(int* arr, int L, int R, vector<vector<int>>& fmap, vector<vector<int>>& gmap) {
	if (fmap[L][R] != -1) return fmap[L][R];
	
	int ans = 0;
	if (L == R) ans = arr[L];
	else {
		int p1 = arr[L] + g2(arr, L + 1, R, fmap, gmap);
		int p2 = arr[R] + g2(arr, L, R - 1, fmap, gmap);
		ans = max(p1, p2);
	}
	fmap[L][R] = ans;
	return ans;
	
}

int g2(int* arr, int L, int R, vector<vector<int>>& fmap, vector<vector<int>>& gmap) {
	if (gmap[L][R] != -1) return gmap[L][R];

	int ans = 0;
	
	if (L != R) {
		int p1 = f2(arr, L + 1, R, fmap, gmap);
		int p2 = f2(arr, L, R - 1, fmap, gmap);
		ans = min(p1, p2);
	}
	gmap[L][R] = ans;
	return ans;

}

//ways 3 严格表递推
int ways3(int* arr, int length) {
	vector<vector<int>> fmap(length + 1, vector<int>(length + 1, 0));
	vector<vector<int>> gmap(length + 1, vector<int>(length + 1, 0));
	for (int i = 0; i < length; i++)
		fmap[i][i] = arr[i];
	for (int startColumn = 1; startColumn < length; startColumn++) {
		int left = 0;
		int right = startColumn;
		while (right  < length) {
			fmap[left][right] = max(arr[left] + gmap[left + 1][right], arr[right] + gmap[left][right - 1]);
			gmap[left][right] = min(fmap[left + 1][right], fmap[left][right - 1]);

			left++;
			right++;
		}
	}
	return max(fmap[0][length - 1], gmap[0][length - 1]);
}
 

整个过程中, 有时出现过很多次三种ways差那么1~2分(上面完整代码里注释的部分).仔细查看原函数才发现我ways1调用f和g时, L 传的时0, 但是R 传的是 length. 所以其实读取范围超出了数组本身范围. 但是c++的尿性又不会像java一样RangeException之类的报错, 所以就出现能跑但是结果不对的情况.
不过呢, 由于可能length位置的数字是0, 导致有些情况结果是正确的.